树状数组(英语:Binary Indexed Tree)又称为二元索引树,由 Fenwick 于 1994年发明,故又称为 Fenwick 树,其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和、区间和。它支持在 O(logn) 的时间复杂度内得到任意前缀和和区间和,同时支持在 O(logn) 的时间复杂度内动态修改单点的值,空间复杂度为 O(n)。 —— wikipedia
树状数组中的精妙操作 —— lowbit(int x)
借助于位运算的lowbit操作(获取整数二进制表示最低位的1),树状数组得以实现其精妙的功能,其精妙之处请看下文。
// lowbit(x) 返回整数x二进制表示最低位的 1
public int lowbit(int x) {
return x & (-x);
}
树状数组求前缀和
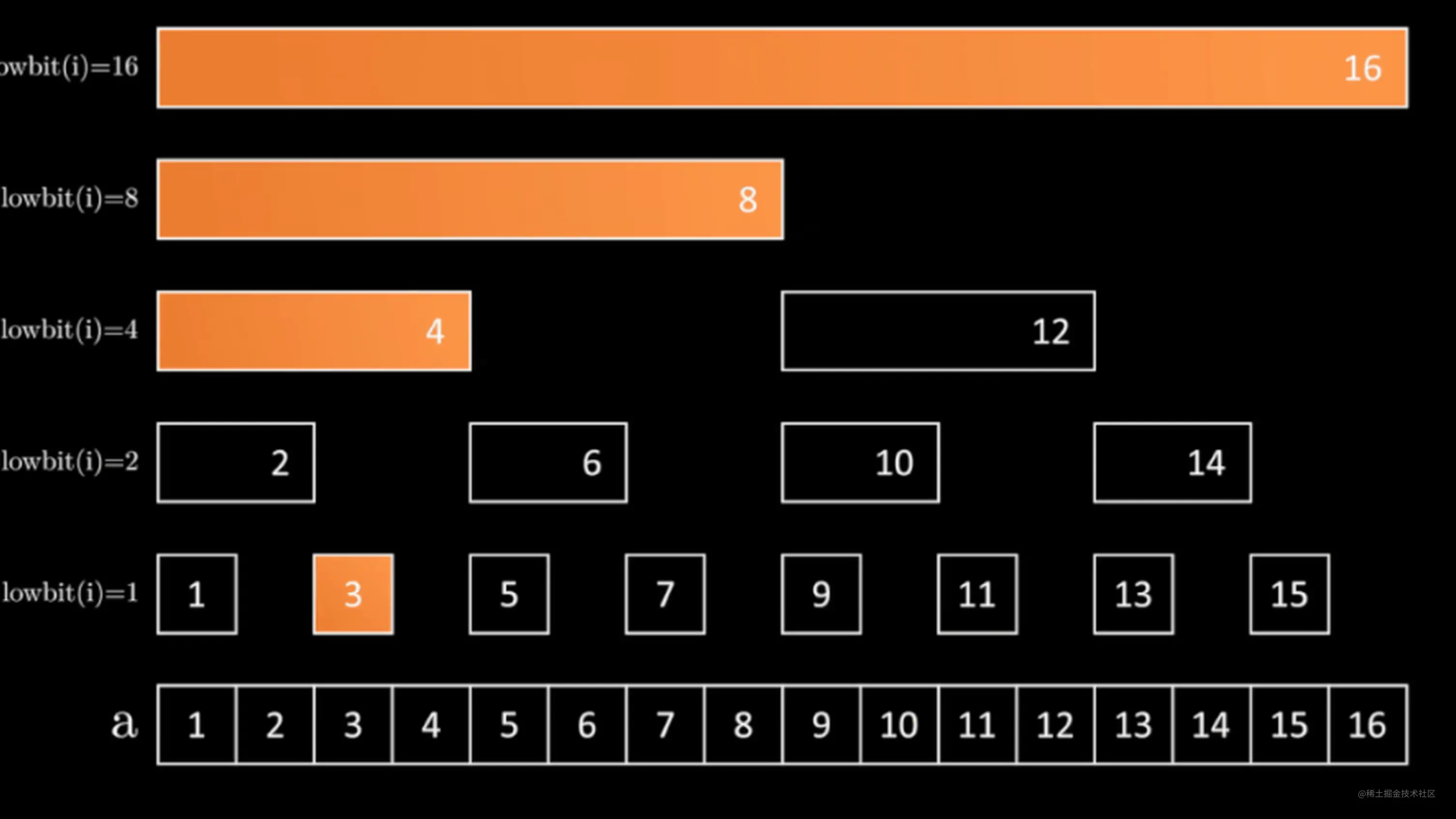
树状数组底层采用数组存储,数组下标从 1 开始 (不使用 0 号元素),如上图所示是一个长度为16且每个元素均为1的数组构造的树状数组,树状数组中 a[i] 保存着一个原数组的区间和(假设原数组是 nums,下标从 1 开始,区间范围是 nums[i – lowbit(i) + 1 : i] 的闭区间)。
如果我们想计算nums[0 : 7] 的和,我们需要计算 a[7] + a[6] + a[4] :
# 计算数组nums 0 到 7 的和: a[7] = nums[7:7] 的和, lowbit(7) = 1,下一个索引为 7 - 1 = 6 a[6] = nums[5:6] 的和, lowbit(6) = 2,下一个索引为 6 - 2 = 4 a[4] = nums[1:4] 的和, lwobit(4) = 4,下一个索引为 4 - 4 = 0
求前缀和的代码:
public int sum(int index) {
if (index <= 0) return 0;
int sum = 0;
while (index > 0) {
sum += arr[index];
index -= lowbit(index);
}
return sum;
}
树状数组求区间和
有了之前求前缀和的基础,求区间和只需要用两个前缀和做差:
public int sum(int l, int r) {
if (r < l) return 0;
return sum(r) - sum(l - 1);
}
树状数组的单点更新
树状数组的单点更新可以转化为增量更新,如上图所示,如果我们想要更新 a[3] , 还要更新 a[3]上面的 a[4], a[8] 以及 a[16]。
那么怎么获取需要更新位置的索引呢?不难发现:
index = 3 4 = 3 + lowbit(3) 8 = 4 + lowbit(4) 16 = 8 + lowbit(8)
所以单点更新的代码可以写成这样:
public void update(int index, int v) {
while (index < arr.length) {
arr[index] += v;
index += lowbit(index);
}
}
如何构造一个树状数组?
树状数组的功能如此强大,前提是能够方便地构造出来。我们可以借助于单点更新的 update 方法来构造树状数组。构造函数传入一个原始数组(下标从 0 开始),设原数组长度为 n,我们创建一个长度为原数组长度 +1 的新数组,然后调用 n 次 update 方法来初始化一个树状数组。
class BIT {
int[] arr;
public BIT(int[] nums) {
int n = nums.length;
this.arr = new int[n + 1];
for (int i = 0; i < n; i++) {
update(i + 1, nums[i]);
}
}
...
}
复杂度对比
| 暴力 | 前缀和 | 树状数组 | |
|---|---|---|---|
| 构造 | O(1) | O(n) | O(nlogn) 做n次加法,每次加法为log n |
| 求和 | O(n) | O(1) | O(logn) |
| 修改 | O(1) | O(n) | O(logn) |
故对于求前缀和和区间和的问题,不需要对原数组进行修改时推荐使用前缀和,需要频繁修改原数组时应使用树状数组。
树状数组的应用
以 LeetCode 307 区域和检索 - 数组可修改 为例 ,解题代码如下:
class NumArray {
BIT bit;
int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
this.bit = new BIT(nums);
}
public void update(int index, int val) {
int v = val - nums[index];
nums[index] = val;
bit.update(index + 1, v);
}
public int sumRange(int left, int right) {
return bit.sum(left + 1, right + 1);
}
private class BIT {
int[] arr;
public BIT(int[] nums) {
this.arr = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
update(i + 1, nums[i]);
}
}
public int lowbit(int x) {
return x & (-x);
}
public void update(int index, int v) {
while (index < arr.length) {
arr[index] += v;
index += lowbit(index);
}
}
public int sum(int index) {
if (index <= 0) return 0;
int sum = 0;
while (index > 0) {
sum += arr[index];
index -= lowbit(index);
}
return sum;
}
public int sum(int l, int r) {
if (r < l) return 0;
return sum(r) - sum(l - 1);
}
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(index,val);
* int param_2 = obj.sumRange(left,right);
*/